Sklearn PCA 降维算法

“维度灾难” 在机器学习中经常会碰到一些高维的数据集，而在高维数据情形下会出现数据样本稀疏，距离计算等困难，这类问题是所有机器学习方法共同面临的严重问题。 特征冗余在高维特征中容易出现特征之间的线性相关。

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。 PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，提取数据的主要特征分量，常用于高维数据的降维。

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
# n_components为特征数目
pca = PCA(n_components=2)

# fit(X) 用数据X来训练PCA模型。transform(X) 降维数据
X_r = pca.fit(X).transform(X)

plt.figure()
colors = ['r', 'g', 'b']

for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, label=target_name)

# legend 标签位置
plt.legend(loc='lower right', shadow=False, scatterpoints=1)
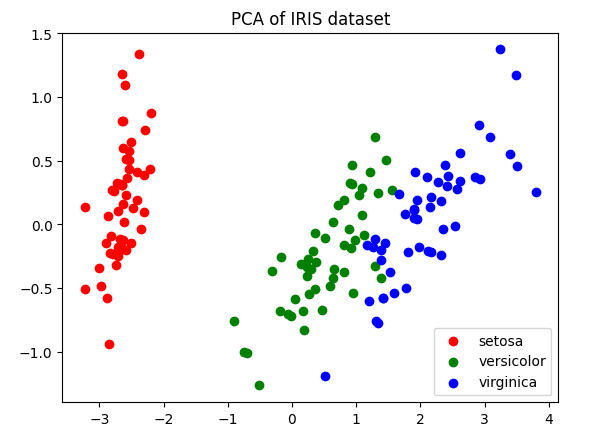
plt.title('PCA of IRIS dataset')