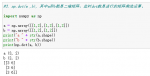
numpy np.vstack() 和 np.hstack() 用法
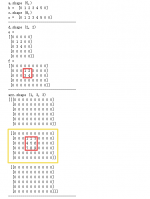
np.vstack():在竖直方向上堆叠。
np.hstack():在水平方向上平铺。
import numpy as np
arr1 = np.array([1,2,3])
arr2 = np.array([4,5,6])
print(np.vstack((arr1,arr2)))
print(‘——————‘)
print(np.hstack((arr1,arr2)))
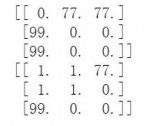
import numpy as np
arr1 = np