关于Java排序算法-归并排序（Merge Sort）

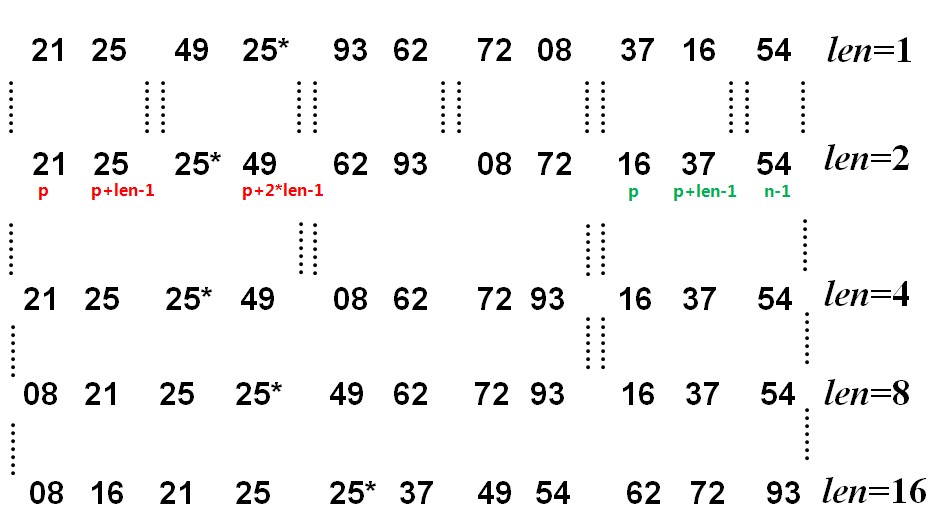
二路归并排序的基本思想：设 n 个待排记录，看成是 n 个有序的子序列，每个子序列的长度为 1 ，对此进行两两归并，得到 n/2 个长度为 2 或 1 的有序子序列；再继续两两归并，得到 n/4 个有序子序列，重复进行直至得到一个长度为 n 的有序序列为止。

public class MergeSort {
  public static void main(String[] args) {
    //int[] arr = { 9, 8, 7, 6, 5, 4, 3, 2, 1 };
    int[] arr = { 21, 25, 49, 25, 93, 62, 72, 8, 37, 16, 54 };

    display("原始数据: ", arr);
    
    mainMerge(arr, arr.length);
    
    display("排序结果: ", arr);
  }

  // 显示
  public static void display(String str, int[] arr) {
    System.out.println(str);
    for (int i = 0; i < arr.length; i++) {
      System.out.print(arr[i] + " ");
    }
    System.out.println();
  }
  
  // 归并排序主算法：
  // 第一趟: arr归并到arrDest；
  // 第二趟: arrDest归并到arr； ......，需偶数趟。
  // 若最后一趟 len>=n，则arrDest直接复制到arr。
  public static void mainMerge(int[] arr, int n) {
    // 对数组arr[n]中的记录进行归并排序
    int[] arrDest = new int[n];
    int len = 1;
    while (len < n) {
      oneMerge(arr, arrDest, n, len);
      len *= 2;
      oneMerge(arrDest, arr, n, len);
      len *= 2;
    }
    // 清空临时数组
    arrDest = null;
  }

  // 一趟归并排序算法：把arr[n]中长度为len的有序表两两归并到arrDest[n]
  public static void oneMerge(int[] arr, int[] arrDest, int n, int len) {
    int p = 0; // 一对待合并表的第一个元素的位置
    
    // 循环两两归并
    while (p + 2 * len - 1 <= n - 1) {
      // twoMerge(int[] arr, int[] arrDest, int s, int m, int t)
      // 将有序表arr[s..m] 和  arr[m+1..t] 归并为有序表arrDest[s..t]
      twoMerge(arr, arrDest, p, p + len - 1, p + 2 * len - 1);
      p += 2 * len;
    }
    
    if (p + len <= n - 1) {
      // 归并最后两个长度不等的有序表
      twoMerge(arr, arrDest, p, p + len - 1, n - 1);
    } else {
      // 复制最后剩下的一个有序表
      for (int i = p; i <= n - 1; i++) {
        arrDest[i] = arr[i];
      }
    }
  }

  // 二路归并算法：将有序表 arr[s..m] 和 arr[m+1..t] 归并为有序表arrDest[s..t]
  public static void twoMerge(int[] arr, int[] arrDest, int s, int m, int t) {
    int i, j, k;
    i = s;
    j = m + 1;
    k = s; // 分别指向每个表的起始位置
    
    // 两个有序表的归并
    while (i <= m && j <= t) {
      if (arr[i] <= arr[j]) {
        arrDest[k] = arr[i];
        i++;
        k++;
      } else {
        arrDest[k] = arr[j];
        j++;
        k++;
      }
    }
    
    // 复制第一个有序表中未归并的元素
    while (i <= m) {
      arrDest[k] = arr[i];
      i++;
      k++;
    }
    
    // 复制第二个有序表中未归并的元素
    while (j <= t) {
      arrDest[k] = arr[j];
      j++;
      k++;
    }
  }

}