微积分的英语 “Calculus” 源自拉丁语,意思是 “小石头”,因为它是从分析小的部分来了解大的整体。
微分是把整体分拆为小部分来求它怎样改变。
积分是把小部分连接(积)在一起来求整体有多大。
1、导数是指 函数图像在某一点处的斜率,是纵坐标增量Δy和横坐标增量Δx在Δx>0时的比值。
2、微分是指 函数图像在某一点处的切线在横坐标取得增量Δx以后,纵坐标取得的增量,一般表示为dy。
3、积分是微分的逆运算,即知道了函数的导函数,反求原函数。
用SymPy库进行测试。
pip install sympy -i https://pypi.tuna.tsinghua.edu.cn/simple/
定义符号变量 x = sp.Symbol(‘x’)
import sympy as sp
import numpy as np
# f的微分
# 求导数 y=3x³+2x²+3
x = sp.Symbol('x')
y = 3*x**3 + 2*x**2 + 3
f = sp.diff(y)
print('y的导数f为:', f)
# f的积分
fy2 = sp.integrate(f, x)
print('f的积分为:', fy2)
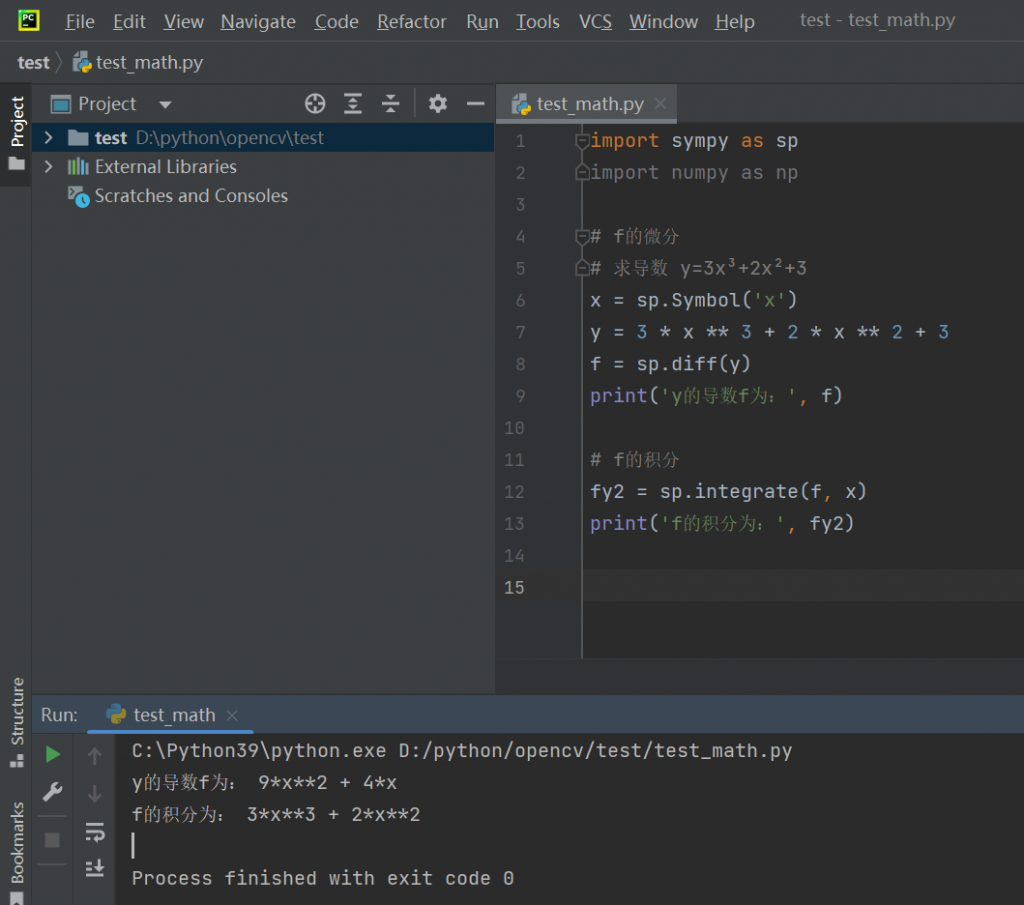
PyCharm如下:
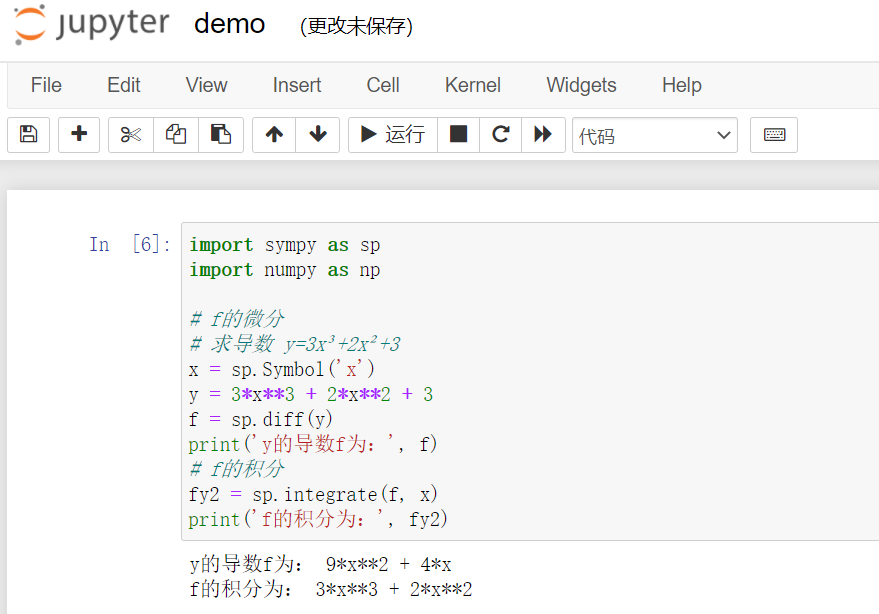
jupyter notebook如下:
感谢york的提醒。示范代码已经修正【2023-02-07】。

博主你好,我在我的环境下运行代码提示:NameError: name ‘x’ is not defined
import sympy as sp
import numpy as np
# f的微分
# 求导数 y=3x³+2x²+3
x = sp.Symbol(‘x’)
y = 3 * x ** 3 + 2 * x ** 2 + 3
f = sp.diff(y)
print(‘y的导数f为:’, f)
# f的积分
fy2 = sp.integrate(f, x)
print(‘f的积分为:’, fy2)
jupyter notebook代码复制的时候少了一句。
# 变量的定义
x = sp.Symbol(‘x’)