回归分析(regression analysis)简称回归,指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
线性回归假设解释变量和响应变量之间存在线性关系,这个线性模型所构成的空间是一个超平面(hyperplane)。超平面是n维欧氏空间中余维度等于1的线性子空间,如平面中的直线、空间中的平面等,总比包含它的空间少一维。
在一元线性回归中,一个维度是响应变量,另一个维度是解释变量,总共两维。因此,其超平面只有一维,就是一条线。
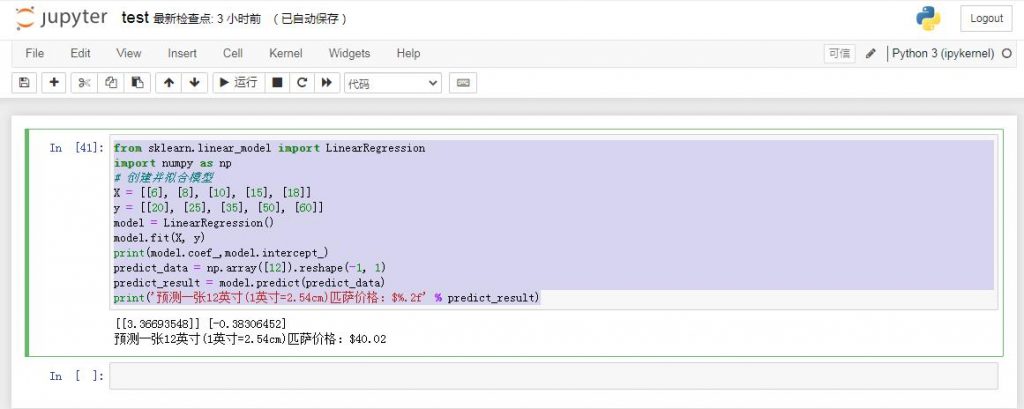
from sklearn.linear_model import LinearRegression
import numpy as np
# 创建并拟合模型
X = [[6], [8], [10], [15], [18]]
y = [[20], [25], [35], [50], [60]]
model = LinearRegression()
model.fit(X, y)
print(model.coef_,model.intercept_)
predict_data = np.array([12]).reshape(-1, 1)
predict_result = model.predict(predict_data)
print('预测一张12英寸(1英寸=2.54cm)匹萨价格:$%.2f' % predict_result)
注意:
reshape(-1, 1) 表示 固定1列,多少行不确定,以实际情况为准。
一元线性回归的模型是y=α+βx,我们要解决的问题就是根据已有的数据估计出参数α和β。 一元线性回归拟合模型的参数估计常用方法是最小二乘法。为了估计出参数α和β,我们首先定义出拟合成本函数,然后对参数进行数理统计。
成本函数(cost function)也叫损失函数(loss function),用来定义模型与观测值的误差。
模型预测的价格与训练集数据的差异称为残差(residuals)或训练误差(training errors)。后面我们会用模型计算测试集,那时模型预测的价格与测试集数据的差异称为预测误差(prediction errors)或测试误差(test errors)。

