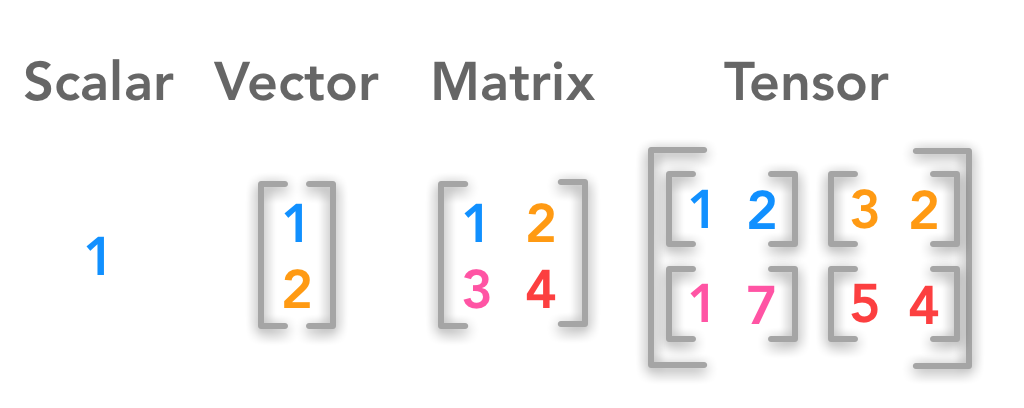
标量(Scalar)、向量(Vector)、矩阵(Matrix)、张量(Tensor)。
1、标量
标量(scalar)：一个标量就是一个单独的数(整数或实数)，不同于线性代数中研究的其他大部分对象(通常是多个数的数组)。
在Python中的定义为：
x = 1
2、向量
向量(vector)：一个向量表示一组有序排列的数，通过次序中的索引我们能够找到每个单独的数。向量中的每个元素就是一个标量，向量中的第i个元素用
表示。
在Python中的定义为：
import numpy as np # 行向量 a = np.array([1,2,3,4])
3、矩阵
矩阵(matrix)：矩阵是一个二维数组，其中的每一个元素由两个索引来决定 
，矩阵通常用加粗斜体的大写字母表示。我们可以将矩阵看做是一个二维的数据表，矩阵的每一行表示一个对象，每一列表示一个特征。
在Python中的定义为：
import numpy as np # 矩阵 a = np.array([[1,2,3], [4,5,6], [7,8,9]])
4、张量
张量(tensor)：超过二维的数组，一般来说，一个数组中的元素分布在若干维坐标的规则网格中，被称为张量。如果一个张量是三维数组，那么我们就需要三个索引来决定元素的位置
，张量通常用加粗的大写字母表示。
import numpy as np # 张量 a = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])