贝叶斯定理 在概率论与统计学中,贝叶斯定理(或称贝叶斯法则、贝叶斯规则)描述了一个事件的可能性,这个可能性是基于预先对于一些与该事件相关的情况的知识。举例来说,如果癌症和年龄有关,那么知道了一个人的年龄的话,使用贝叶斯定理,相比于根本不了解关于此人的任何其他信息,就可以更准确地帮助评估这个人得癌症与否的概率。
贝叶斯定理所阐述的也就是后验概率的获得方法。
用数学公式来表述贝叶斯定理:
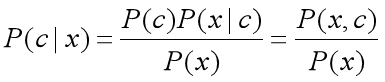
c表示的是随机事件发生的一种情况。x表示的就是证据(evidence),泛指与随机事件相关的因素。
P(c|x):在x条件下,随机事件出现c情况的概率,(后验概率)。
P(c):(不考虑相关因素)随机事件出现c情况的概率,(先验概率)。
P(x|c):在已知事件出现c情况的条件下,条件x出现的概率,(后验概率)。
P(x):x出现的概率,(先验概率)。
何为“朴素”? “朴素”(naive)指的是属性条件独立性假设。因为我们为了能够获得合理的p(c|x)的值,采用了“很不科学”的假设,即事件的各个属性不相关,称为属性条件独立性假设。这个假设用公式表达是这样的:
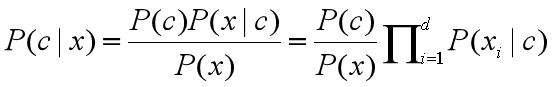
公式的左边等式就是我们熟悉的贝叶斯定理的公式,而右边新加的一个式子是将P(x|c)(条件联合概率)表达成了 ![]()
(多个条件概率的相乘)。用俗话说,这个假设认为每个属性取它的各个值的可能性是独立的,与其它属性的取值不相关。
在scikit-learn中,一共有3个朴素贝叶斯的分类算法类。分别是:
GaussianNB 先验为高斯分布(正态分布)的朴素贝叶斯。
MultinomialNB 先验为多项式分布的朴素贝叶斯。
BernoulliNB 先验为伯努利分布的朴素贝叶斯。
一般来说,如果样本特征的分布大部分是连续值,使用GaussianNB会比较好。如果如果样本特征的分布大部分是多元离散值,使用MultinomialNB比较合适。而如果样本特征是二元离散值或者很稀疏的多元离散值,应该使用BernoulliNB。 关于分类,我们仍然使用了Iris数据集,Iris数据集给出的三种花是按照顺序来的,前50个是第0类,51-100是第1类,101~150是第二类,如果我们分训练集和测试集的时候要把顺序打乱。
# 导入高斯模型 from sklearn.naive_bayes import GaussianNB import numpy as np # 定义预测变量与目标变量 x= np.array([[-3,7],[1,5], [1,2], [-2,0], [2,3], [-4,0], [-1,1], [1,1], [-2,2], [2,7], [-4,1], [-2,7]]) Y = np.array([3, 3, 3, 3, 4, 3, 3, 4, 3, 4, 4, 4]) # 创建高斯分类器 model = GaussianNB() # 使用刚才定义的训练集训练模型 model.fit(x, Y) # 预测并输出 predicted= model.predict([[1,2],[3,4]]) print (predicted)
# 创建多项式分类器 from sklearn.naive_bayes import MultinomialNB import numpy as np # 定义预测变量与目标变量 X = np.random.randint(5, size=(6, 10)) print (X) y = np.array([1, 2, 3, 4, 5, 6]) clf = MultinomialNB() clf.fit(X, y) # 预测并输出 predicted = clf.predict(X[2:]) print (predicted)
# 创建伯努利分类器 from sklearn.naive_bayes import BernoulliNB import numpy as np # 定义预测变量与目标变量 X = np.random.randint(2, size=(6, 10)) Y = np.array([1, 2, 3, 4, 4, 5]) clf = BernoulliNB() clf.fit(X, Y) # 预测并输出 print(clf.predict(X[2:]))
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import naive_bayes
iris = datasets.load_iris()
X = iris["data"]
y = iris["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 样本特征的分布大部分是连续值,因此使用GaussianNB,如果样本是离散值则选择MultinomialNB或BernoulliNB
Model = naive_bayes.GaussianNB()
Model.fit(X_train, y_train)
predict = Model.predict(X_test)
print(predict)
print(y_test)
score = Model.score(X_test, y_test)
print('the score is :', score)
randint函数说明
numpy.random.randint(low, high=None, size=None, dtype=’l’)
输入:
low 为最小值。
high 为最大值。
size 为数组维度大小。
dtype 为数据类型,默认的数据类型是np.int。
返回值:
返回随机整数或整型数组,范围区间为[low,high),包含low,不包含high;
high没有填写时,默认生成随机数的范围是[0,low)。
