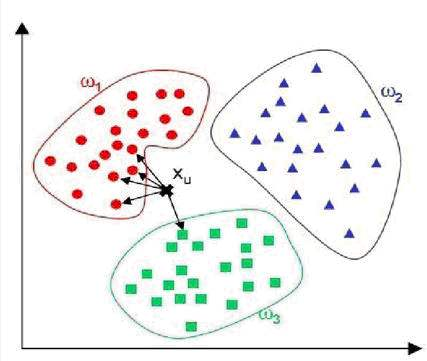
K近邻法(k-nearest neighbors,KNN)是一种很基本的机器学习方法,在我们平常的生活中也会不自主的应用。比如,我们判断一个人的人品,只需要观察他来往最密切的几个人的人品好坏就可以得出了。这里就运用了KNN的思想。KNN方法既可以做分类,也可以做回归。
KNN做回归和分类的主要区别在于最后做预测时候的决策方式不同。KNN做分类预测时,一般是选择多数表决法,即训练集里和预测的样本特征最近的K个样本,预测为里面有最多类别数的类别。而KNN做回归时,一般是选择平均法,即最近的K个样本的样本输出的平均值作为回归预测值。由于两者区别不大,虽然本章主要是讲解KNN的分类方法,但思想对KNN的回归方法也适用。由于scikit-learn里只使用了蛮力实现(brute-force),KD树实现(KDTree)和球树(BallTree)实现。
KNN算法我们主要要考虑三个重要的要素,对于固定的训练集,只要这三点确定了,算法的预测方式也就决定了。这三个最终的要素是k值的选取,距离度量的方式和分类决策规则。 对于分类决策规则,一般都是使用前面提到的多数表决法。所以我们重点关注的是k值的选择和距离的度量方式。
一、k值的选择
对于k值的选择,没有一个固定的经验,一般根据样本的分布,选择一个较小的值,可以通过交叉验证选择一个合适的k值。
选择较小的k值,就相当于用较小的领域中的训练实例进行预测,训练误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是泛化误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
选择较大的k值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少泛化误差,但缺点是训练误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。一个极端是k等于样本数m,则完全没有分类,此时无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的类,模型过于简单。
二、距离的度量方式
欧式距离、曼哈顿距离、闵可夫斯基距离。

三、代码
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn import datasets
import numpy as np
iris = datasets.load_iris()
X = iris["data"]
y = iris["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 定义一个KNN分类器对象
knn = KNeighborsClassifier()
# 调用该对象的训练方法
knn.fit(X_train, y_train)
# 调用该对象的测试方法,得到预测结果
iris_y_predict = knn.predict(X_test)
# 计算各测试样本基于概率的预测值
probility = knn.predict_proba(X_test)
# 计算与最后一个测试样本距离最近的5个点,返回的是这些样本的序号组成的数组
neighborpoint = knn.kneighbors([X_test[-1]],5,False)
# 调用该对象的打分方法,计算出准确率
score = knn.score(X_test,y_test,sample_weight=None)
# 输出测试的结果
print('iris_y_predict = ')
print(iris_y_predict)
# 输出原始测试数据集的正确标签,以方便对比
print('iris_y_test = ')
print(y_test)
# 输出准确率计算结果
print('Accuracy:',score)
# 输出最后测试样本距离最近的5个训练点序号
print('neighborpoint of last test sample:',neighborpoint)
# 输出各测试样本基于概率的预测值
print('probility:',probility)
#print(X_test[-1].reshape(-1,1))
